I'll demonstrate how to simulate a floor in Simmechanics, this floor will prevent free falling (6 DOF) objects from falling below a threshold level ("the floor level"), i.e. I will simulate a collision/interaction between the free falling object and the floor.
I'll assume you have a basic understanding of how Simmechanics works. If you don't, you might want to check this post.
The problem
If you have used Simmechanics before, then you know it's an excellent toolbox for simulation of multibody dynamics. You can easily work with robotic arms, which are always fixed to the ground. But what happens when you want to work with legged robots, that can't be fixed to the ground. Well, then you run in a problem, if you don't fix any part of the robot to the ground, then the robot will fall and fall by action of the gravity. Removing the gravity is not an option, because you want to design the controllers of your robot with gravity compensation, even worse your robot will float if you simulate a zero gravity environment.
Let's develop a minimal model to illustrate the problem: a 6 DOF ball.
Illustrating the problem
We'll start by drawing the floor. Implement the following block diagram in Simulink.
Block diagram to visualize the floor.
Modify the Floor block parameters to match the following image, and also on the Visualization tab change the Body geometry option to "Equivalent ellipsoid from mass properties".
Parameters to draw a 1 meter radius floor.
Next, start a simulation. Activate the the Isometric View and the "Enable Automatic Expanding Fit".
Animation showing the floor as a 1 m radius disk.
Now, we add the free falling ball. Add more blocks to the model to match the following diagram.
Added a free falling ball to the model.
Next, modify the parameters of the Above Ground block and the Ball block, to match the following images. On the Visualization tab of the ball block also select "Equivalent ellipsoid from mass properties" on the Body geometry option.
Above Ground parameters
|
Ball parameters
|
Now simulate the system and observe the problem.
Ball falling through the floor.
The Idea
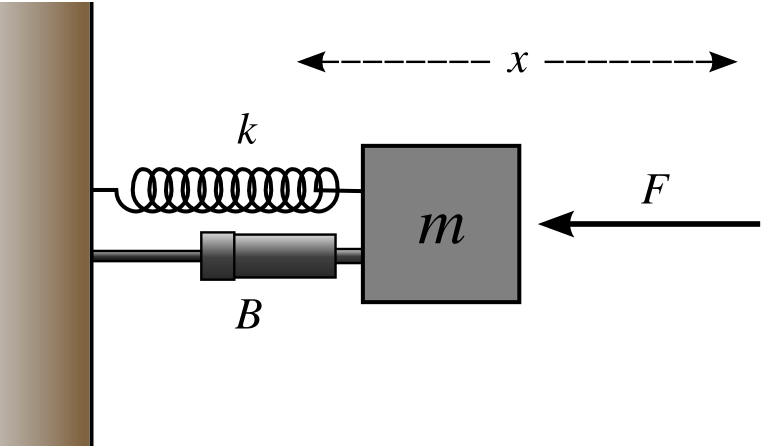
Known the problem, we must now create a solution. Let's begin by analyzing how the floor behaves. Ideally the floor is a rigid body that exerts enough force over adjacent bodies to prevent them from falling through. Now, perfect rigid bodies doesn't exist in the real world, all bodies deform when stressed or compressed. This means our floor model must be elastic, this can be modeled as a spring.
Our floor model can't be modeled only as a spring, otherwise will end with a trampoline. When we fall to the ground, we don't jump back to the sky, instead our potential energy dissipates as heat or as permanent deformation. This means our floor model must also have a dissipation element.
A mass-spring-damper system.
That description resembles a lot to a mass-spring-damper system. As you might know those system tend to vibrate, unless they are overdamped. This means our floor model must behave as an overdamped mass-spring-damper system. The final condition is that the free falling object must be the mass of the system, this means that our floor model doesn't really has a mass parameter. Other way to think of it is that the mass is detachable, and this mass is only affected by the spring and the damper when is at or below the floor level.
Implementing the floor interaction
First, let's enable some sensor/actuator ports on the free falling ball. These two ports must be located at the same point, at the bottom of the ball.
Adding sensor/actuator ports to the free falling ball.
The floor control diagram can be implemented as follows:
Floor Control Diagram.
The body sensor is configured to output the position in meters, while the body actuator is configured to exert force in newtons over the ball. Using a demuxer, we extract the Y component of the position, then we compare it to the floor level. If the Y position of the bottom of the ball is below the floor level, then we activate the spring-damper system represented by the gains 'k' and 'c', otherwise the floor exerts no force over the ball. The force developed by the spring damper system is exerted over the ball but only in the Y direction, thanks to a muxer and the body actuator.
The final step is selecting 'k' and 'c'. You need to considerate the following things:
- The damping ratio "c / 2 / sqrt(m * k)" should be greater than 1, to guarantee overdamping.
- The free falling body will sink a distance "m * g / k" into the ground, so you might want to increase 'k', right?
- But Increasing 'k', also increases the computation load of the simulation.
How do I select the parameters 'k' and 'c'? I first select 'k' balancing how much sinking and computation load can I tolerate. Then I compute 'c' using the biggest mass and choosing a damping ratio of 1.
The Results
I'll leave you with the simulation output.
Floor control enabled.
Ball interacting with the floor. (Y position)
As a closing remark, I must say that I have used this method in the simulation of a humanoid robot with positive results.












Jorge,
ReplyDeleteHow did you go about modelling the floor? What values did you input for the blocks in your SimMechanics block diagram?
Hey there,
DeleteFor the spring constant 'k', I used the floor material (say concrete) young's modulus times the "contact area", and for the friction coefficient 'c' I selected a value that results in critically damped oscillation.
Hope that helps
Selling USA FRESH SPAMMED SSN Leads/Fullz, along with Driving License/ID Number with EXCELLENT connectivity.
Delete**PRICE**
>>1$ FOR EACH FULLZ WITHOUT DL NUMBER
>>2$ FOR EACH LEAD/FULLZ/PROFILE
>>5$ FOR EACH PREMIUM LEAD/FULLZ/PROFILE
**DETAILS IN EACH LEAD/FULLZ**
->FULL NAME
->SSN
->DATE OF BIRTH
->DRIVING LICENSE NUMBER WITH EXPIRY DATE
->ADDRESS WITH ZIP
->PHONE NUMBER, EMAIL, I.P ADDRESS
->EMPLOYEE DETAILS
->REALTIONSHIP DETAILS
->MORTGAGE INFO
->BANK ACCOUNT DETAILS
>All Leads are Tested & Verified.
>Invalid info found, will be replaced.
>Serious buyers will be welcome & I will give discounts on bulk orders.
>Fresh spammed data of USA Credit Bureau
>Good credit Scores, 700 minimum scores
>Bulk order will be preferable
>Minimum order 20 leads/fullz
>Hope for the long term business
>You can asked for samples, specific states & zips (if needed)
>Payment mode BTC, ETH, LTC, Paypal & PERFECT MONEY
Email > leads.sellers1212@gmail.com
Telegram > @leadsupplier
ICQ > 752822040
''OTHER GADGETS PROVIDING''
>SSN Fullz
>Dead Fullz
>Carding Tutorials
>Hacking Tutorials
>SMTP Linux Root
>DUMPS with pins track 1 and 2
>Sock Tools
>Server I.P's
>USA emails with passwords (bulk order preferable)
**Contact 24/7**
Email > leads.sellers1212@gmail.com
Telegram > @leadsupplier
ICQ > 752822040
Verified=Tools=Available
DeleteKali Linux Master Class
D33p/D@rk Web Complete Course
Spamming Tools/Tutorials
BTC Cracker/Flasher
Key LOggers
Hacking Stuff/Books/Tuts
SMTP's
RDP's
C-panel's
Shells
Web-mailers
Mailers/Senders/Bomber
Combos
Carding Cashout/Spamming Methods
Brutes
Premium Cracked Versions
Viruses/RAT's
Scam Page Scripting
7528 22040 I.C.Q
@killhacks Tel Gr
Fresh Spammed & Legit Fullz/Pros/Leads
High CS Fullz (700+)
CC Fullz
SSN+DOB FULLZ
SSN+DOB+DL+Emp Details Fullz
Premium Fullz
Dumps With Pin Codes 101/202 (Good Balanced)
Business Fullz with EIN
7528 22040 I.C.Q
@killhacks Tel Gr
All stuff will be legit & Verified
Invalid found will be replace instantly
Just hit me up Guys
NAME|SSN|DOB|DL|ADDRESS|EMAIL|PHONENUMBER|WORKHISTORY|ACCOUNTDETAILS
DeleteFresh Fullz & Fresh Spammed
CCNUMBER|MM|YYYY|CVV|NAME|SSN|DOB|ADDRESS|EMAIL|PHONENUMBER
CC fullz with CVV
High Credit Scores Pros 700+
EIN Business Fullz
ICQ 752822040
WA/TG +92 317 272 1122
TG @leadsupplier
Skype/Wickr @peeterhacks
Spamming All fresh Tools & Tutorials
Hacking Stuff
Carding Methods & Cashout Methods
Loan Methods
SMTP's/RDP's/SHELLS/Brutes/C-panels
Key-Loggers/Kali-Linux Full Package
Courses for D**K/D**P Web
SQLi Injector
Combos/I.P's/Proxies
Logs/HQ Emails
ICQ/TG @killhacks
WA +92 317 272 1122
exploit.tools4u at gmail dot com
Hey,
ReplyDeleteI just stumbled over your site and find your Simulations very interesting!
I am currently trying to get into Simmechanics but have a few starting problems.
Can you please send me the mdl file of this simulation?
that would really be of great help for me!
Kind regards, Thomas
Hey Jorge,
ReplyDeletethanks so much for your nice explanation. I am writing my diploma thesis about pretty much the same thing as you did with your humanoid robot simulation and this tutorial just blew away one of the many problems i am encountering. ;)
In addition i think i found a little mistake in the explanation above:
The equation for calculating the damping ratio you mentioned above "c / 2 / sqrt(m * k)"
should look like this "c / (2*sqrt(m * k))"
Cheers
great work. can u share the value of k and c in your system ?
ReplyDeletethank you so much
I build up this model in simmechanics model. But unfortunately with the "derivative" block (the forceconsisted from spring and damping was almost proportional and ball fell down) it didn't work properly so i exchange it to the "Switched
ReplyDeletederivative for
linearization" block and it started to work. Any idea why?
Hola Jorge, Estoy Siguiendo tu Blog, y Este trabajo de simular un piso en SimMechanics es muy bueno, favor me pordías ayudar de como Simular piernas de Robot Bípedo para la Camita, Agradeceria Mucho tu ayuda.
ReplyDeleteSaludo,
Josmell Alva.
Great post! I am actually getting ready to across this information, It's very helpful for this blog.
ReplyDeletethank you for your sharing!
goldenslot casino
บาคาร่าออนไลน์
gclub casino
This comment has been removed by the author.
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteCustom eCommerce Web Design London UK, Hire Ecommerce Developers Lucknow India, eCommerce Website Development Services USA
ReplyDeleteHello! This is my first visit to your blog! We are a team of volunteers and starting a new initiative in a community in the same niche. Your blog provided us useful information to work on. You have done an outstanding job.
ReplyDeleteHadoop Training in Bangalore
Hadoop Training in Chennai
When I initially commented, I clicked the “Notify me when new comments are added” checkbox and now each time a comment is added I get several emails with the same comment. Is there any way you can remove people from that service? Thanks.
ReplyDeleteBig data training in tambaram
I simply wanted to write down a quick word to say thanks to you for those wonderful tips and hints you are showing on this site.
ReplyDeletejava training in chennai
java training in bangalore
java online training
java training in pune
java training in chennai
java training in bangalore
java training in tambaram
Hi there I am so thrilled I found your website, I really found you by mistake, while I was browsing on Yahoo for something else, Anyhow I am here now and would just like to say thanks a lot for a tremendous post and an all-round exciting blog (I also love the theme/design), I don’t have time to go through it all at the minute but I have saved it and also added in your RSS feeds, so when I have time I will be back to read more, Please do keep up the awesome job.
ReplyDeleteBig data training in tambaram
Hadoop Training in Bangalore
Hadoop Training in Chennai
A very nice guide. I will definitely follow these tips. Thank you for sharing such detailed article. I am learning a lot from you.
ReplyDeleteData Science training in btm
Data Science training in rajaji nagar
Data Science training in chennai
Data Science training in kalyan nagar
Data Science training in electronic city
Data Science training in USA
selenium training in chennai
selenium training in bangalore
Nice post. By reading your blog, i get inspired and this provides some useful information. Thank you for posting this exclusive post for our vision.
ReplyDeleterpa training in Chennai
rpa training in Chennai
rpa training in Chennai
rpa training in velachery
rpa training in tambaram
rpa training in sholinganallur
rpa training in anna nagar
rpa online training
I am so proud of you and your efforts and work make me realize that anything can be done with patience and sincerity. Well I am here to say that your work has inspired me without a doubt.
ReplyDeletepython training in tambaram
python training in annanagar
python training in OMR
I think you have a long story to share and i am glad after long time finally you cam and shared your experience.
ReplyDeletejava training in marathahalli | java training in btm layout
java training in jayanagar | java training in electronic city
Hello I am so delighted I found your blog, I really found you by mistake, while I was looking on Yahoo for something else, anyways I am here now and would just like to say thanks for a tremendous post. Please do keep up the great work.
ReplyDeletejava training in chennai | java training in bangalore
java training in tambaram | java training in velachery
Thanks for the good words! Really appreciated. Great post. I’ve been commenting a lot on a few blogs recently, but I hadn’t thought about my approach until you brought it up.
ReplyDeletePython training in usa
Python training in marathahalli
Python training in pune
I am really impressed with your efforts and really pleased to visit this post.
ReplyDeleteData Science course in kalyan nagar | Data Science course in OMR
Data Science course in chennai | Data science course in velachery
Data science online course | Data science course in jaya nagar
Your new valuable key points imply much a person like me and extremely more to my office workers. With thanks from every one of us.
ReplyDeleteBest AWS Training in Chennai | Amazon Web Services Training in Chennai
AWS Training in Bangalore | Amazon Web Services Training in Bangalore
Amazon Web Services Training in Pune | Best AWS Training in Pune
Your new valuable key points imply much a person like me and extremely more to my office workers. With thanks from every one of us.
Thank you a lot for providing individuals with a very spectacular possibility to read critical reviews from this site.
ReplyDeleteBlueprism training in Pune
Blueprism training in Chennai
Your article gives lots of information to me. I really appreciate your efforts admin, continue sharing more like this.
ReplyDeleteDevOps Training in Chennai
DevOps course in Chennai
RPA Training in Chennai
Blue Prism Training in Chennai
UiPath Training in Chennai
AWS Training in Chennai
Angularjs Training in Chennai
Lovely blog with much more interesting article, I will keep on reading your update. Thanks for the share Web Developers in Bangalore | Website Developers in Bangalore | Web Designers in Bangalore Bangalore
ReplyDeleteThis is the best article on recent technology. Thanks for taking your own time to share your knowledge.
ReplyDeleteSelenium Training in Chennai
Best selenium training in chennai
iOS Training in Chennai
Digital Marketing Training in Chennai
best big data training in chennai
big data training institute in chennai
Hadoop Training in Velachery
This was helpful to me thanks for sharing this useful information. Kindly continue the work.
ReplyDeleteFrench Institute in Chennai
French Language Course in Chennai
French Training in Chennai
French Coaching near me
German Training in Chennai
German Classes in Chennai
German Language Course in Chennai
Amazon has a simple web services interface that you can use to store and retrieve any amount of data, at any time, from anywhere on the web. Amazon Web Services (AWS) is a secure cloud services platform, offering compute power, database storage, content delivery and other functionality to help businesses scale and grow.For more information visit.
ReplyDeleteaws online training
aws training in hyderabad
aws online training in hyderabad
I am really enjoying reading your well written articles.
ReplyDeleteIt looks like you spend a lot of effort and time on your blog.
I have bookmarked it and I am looking forward to reading new articles. Keep up the good work..
Java Training in Bangalore
Best Java Training Institutes in Bangalore
Java Course in Bangalore
Java Training Institutes in Bangalore
hadoop course in bangalore
best hadoop training institutes in bangalore
best big data training in bangalore
hadoop classes in bangalore
This post is marvelous!!! I read this blog very great content and i learn more details. Thank you so much.
ReplyDeleteBig Data Hadoop Training institutes in Bangalore
Big Data Hadoop Training institute in Bangalore
Best Big Data Hadoop Training in Bangalore
Big Data Hadoop Training in Chennai Velachery
Big Data Hadoop Training in Tnagar
Big Data Hadoop Course in Nungambakkam
Big Data Hadoop Course in karappakkam
Big Data Hadoop Training in padur
Big Data Hadoop Training in Chennai
Whoa! I’m enjoying the template/theme of this website. It’s simple, yet effective. A lot of times it’s very hard to get that “perfect balance” between superb usability and visual appeal. I must say you’ve done a very good job with this.
ReplyDeleteAWS Training in Velachery | Best AWS Course in Velachery,Chennai
Best AWS Training in Chennai | AWS Training Institutes |Chennai,Velachery
Amazon Web Services Training in Anna Nagar, Chennai |Best AWS Training in Anna Nagar, Chennai
Amazon Web Services Training in OMR , Chennai | Best AWS Training in OMR,Chennai
Amazon Web Services Training in Tambaram, Chennai|Best AWS Training in Tambaram, Chennai
AWS Training in Chennai | AWS Training Institute in Chennai Velachery, Tambaram, OMR
Amazing information,thank you for your ideas.after along time i have studied an interesting information's.we need more updates in your blog.
ReplyDeletePython Training in T nagar
Python Certification Training in T nagar
best python training in bangalore
python training in bangalore
Thank you for sharing this valuable information with us. I am really impressed with your work.
ReplyDeleteIoT Courses
Internet of Things Training
IoT Training
Internet of Things Training in Adyar
Internet of Things Training in Velachery
Internet of Things Training in Tambaram
Lovely blog with much more interesting article, I will keep on reading your update. Thanks for the share Web Designers in Bangalore | Website Designers in Bangalore | Website Design in Bangalore Bangalore
ReplyDeleteThanks for such a great article here. I was searching for something like this for quite a long time and at last I’ve found it on your blog. It was definitely interesting for me to read about their market situation nowadays. Well written article Thank You for Sharing with Us pmp training in velachery | project management certfication in chennai | project management training institute in chennai
ReplyDeleteเผาผลาญไขมัน ไม่มีอันตราย เป็นเทคโนโลยี ที่มีคุณภาพสูงสำหรับเพื่อการเผาผลาญไขมันส่วนเกิน
ReplyDeleteเครื่องจะตรวจค้นจำนวนไขมัน และก็คำนวนพลังงานที่จำต้องใช้อัตโนมัติ และก็พวกเราจะใช้เครื่องใช้ไม้สอยยิงคลื่น
อัลตร้าซาวด์เข้าไปในรอบๆที่ได้ทำเครื่องหมายไว้อย่างสม่ำเสมอ โดยไม่เจ็บต่อเยื่อรอบๆ ใกล้เคียง ไม่ว่าจะเป็นผิวหนังข้างบน เซลล์ประสาท หรือ เส้นเลือด ต่อจากนั้นเซลล์ไขมันจะถูกแปลงให้เป็นของเหลวแล้วถูกซึมซับไปสู่กระแส เลือด แล้วถูกนำไปเผาผลาญโดยระบบการกำจัดไขมันของ
ร่างกายตามธรรมชาติ ทำให้ท่านสัมผัสได้ถึงรูปร่างที่กระชับแล้วก็เรียบเนียนขึ้นโดยทันทีข้างหลังการดูแลและรักษา โดยไม่เป็นผลใกล้กันอะไรก็ตามต่อสุขภาพร่างกายรวมทั้งสามารถดำเนิน
ชีวิตตามเดิม โดยไม่ต้องพักรักษาตัว
สลายไขมัน กระชับสัดส่วน
สลายไขมัน ไม่ผ่าตัด
Excellent blog about Embedded program, keep sharing more like this.
ReplyDeleteR Training in Chennai
R Programming Training in Chennai
RPA courses in Chennai
AWS Certification in Chennai
DevOps Certification Chennai
Angular 6 Training in Chennai
Awesome Post. The content showcases your in-depth knowledge. Pls keep on writing.
ReplyDeleteIELTS coaching in Chennai
IELTS Training in Chennai
IELTS coaching centre in Chennai
Best IELTS coaching in Chennai
IELTS classes in Chennai
Best IELTS coaching centres in Chennai
IELTS Centre in Chennai
IELTS Training
IELTS Course in Chennai
Very informative post. Thanks for sharing.
ReplyDeleteC C++ Training in Chennai | C Training in Chennai | C++ Training in Chennai | C++ Training | C Language Training | C++ Programming Course | C and C++ Institute | C C++ Training in Chennai | C Language Training in Chennai
Amazing Blog. The liked your way of writing. It is easy to understand. Waiting for your next post.
ReplyDeleteNode JS Training in Chennai
Node JS Course in Chennai
Node JS Advanced Training
Node JS Training Institute in chennai
Node JS Training Institutes in chennai
Node JS Course
Informatica Training in Chennai
Informatica Training center Chennai
Informatica Training Institute in Chennai
You have done a great job!!! by explore your knowledge with us.
ReplyDeleteselenium training in velachery
Selenium Training in Chennai
Big Data Training in Chennai
web designing training in chennai
Loadrunner course in Chennai
Best Loadrunner training institute in chennai
WOW Awesome Information, I like your Post. Thanks for Information
ReplyDeleteNice informative post...Thanks for sharing..
ReplyDeleteArticle submission sites
Education
ReplyDeleteAmazing write-up. The content is very interesting, waiting for your future write-ups.
Html5 Training in Chennai
Html5 Courses in Chennai
Html5 Training
Html5 Course
Html5 Training Course
Drupal Training in Chennai
Drupal Certification Training
Drupal 8 Training
Drupal 7 Training
Great effort! Clear and precise content. Hoping for more posts from you. Regards.
ReplyDeleteMicrosoft Dynamics CRM Training in Chennai | Microsoft Dynamics Training in Chennai | Microsoft Dynamics CRM Training | Microsoft Dynamics CRM Training institutes in Chennai | Microsoft Dynamics Training | Microsoft CRM Training | Microsoft Dynamics CRM Training Courses | CRM Training in Chennai
Thanks for your post. This is excellent information. The list of your blogs is very helpful for those who want to learn, It is amazing!!! You have been helping many application.
ReplyDeletebest selenium training in chennai | best selenium training institute in chennai selenium training in chennai | best selenium training in chennai | selenium training in Velachery
Outstanding blog thanks for sharing such wonderful blog with us ,after long time came across such knowlegeble blog. keep sharing such informative blog with us.
ReplyDeletemachine learning course in Chennai
machine learning training center in Chennai
machine learning with python course in Chennai
Hello all
ReplyDeleteam looking few years that some guys comes into the market
they called themselves hacker, carder or spammer they rip the
peoples with different ways and it’s a badly impact to real hacker
now situation is that peoples doesn’t believe that real hackers and carder scammer exists.
Anyone want to make deal with me any type am available but first
I‘ll show the proof that am real then make a deal like
Available Services
..Wire Bank Transfer all over the world
..Western Union Transfer all over the world
..Credit Cards (USA, UK, AUS, CAN, NZ)
..School Grade upgrade / remove Records
..Spamming Tool
..keyloggers / rats
..Social Media recovery
.. Teaching Hacking / spamming / carding (1/2 hours course)
discount for re-seller
Contact: 24/7
fixitrogers@gmail.com
This guy is real I already deal with him
DeleteI think this is the best article today about the future technology. Thanks for taking your own time to discuss this topic, I feel happy about that curiosity has increased to learn more about this topic. Artificial Intelligence Training in Bangalore. Keep sharing your information regularly for my future reference.
ReplyDeleteVery good to read thanks for sharing
ReplyDeleteR programming training institute chennai
Hello all
ReplyDeleteam looking few years that some guys comes into the market
they called themselves hacker, carder or spammer they rip the
peoples with different ways and it’s a badly impact to real hacker
now situation is that peoples doesn’t believe that real hackers and carder scammer exists.
Anyone want to make deal with me any type am available but first
I‘ll show the proof that am real then make a deal like
Available Services
..Wire Bank Transfer all over the world
..Western Union Transfer all over the world
..Credit Cards (USA, UK, AUS, CAN, NZ)
..School Grade upgrade / remove Records
..Spamming Tool
..keyloggers / rats
..Social Media recovery
.. Teaching Hacking / spamming / carding (1/2 hours course)
discount for re-seller
Contact: 24/7
fixitrogers@gmail.com
Very nice post here and thanks for it .I always like and such a super contents of these post.
ReplyDeleteExcellent and very cool idea and great content of different kinds of the valuable information's.
data science online training
python online training
uipath online training
data science with python online training
rpa online training
Thanks for such a great article here. I was searching for something like this for quite a long time and at last I’ve found it on your blog. It was definitely interesting for me to read about their market situation nowadays.
ReplyDeleteMicrosoft Azure online training
Selenium online training
Java online training
Java Script online training
Share Point online training
It was worth visiting your blog and I have bookmarked your blog. Hope to visit again
ReplyDeleteangularjs online training
apache spark online training
informatica mdm online training
devops online training
aws online training
Thank you for an additional great post. Exactly where else could anybody get that kind of facts in this kind of a ideal way of writing? I have a presentation next week, and I’m around the appear for this kind of data.
ReplyDeletedevops online training
aws online training
data science with python online training
data science online training
rpa online training
Amazing Post. Great use of words. The idea you shared shows your knowledge depth. Thanks for Sharing.
ReplyDeleteHadoop Admin Training in Chennai
Hadoop Administration Training in Chennai
Big Data Administrator Training
Hadoop Administration Course
Hadoop Admin Training in OMR
Hadoop Admin Training in Anna Nagar
Hello, I read your blog occasionally, and I own a similar one, and I was just wondering if you get a lot of spam remarks? If so how do you stop it, any plugin or anything you can advise? I get so much lately it’s driving me insane, so any assistance is very much appreciated.
ReplyDeleteData science Course Training in Chennai |Best Data Science Training Institute in Chennai
AWS Course Training in Chennai |Best AWS Training Institute in Chennai
Devops Course Training in Chennai |Best Devops Training Institute in Chennai
Selenium Course Training in Chennai |Best Selenium Training Institute in Chennai
This comment has been removed by the author.
ReplyDeleteThis is the best post for developing my knowledge and Keep posting. Thank you for sharing with us...!
ReplyDeleteSpark Training in Chennai
Spark Training
Pega Training in Chennai
Primavera Training in Chennai
Unix Training in Chennai
Linux Training in Chennai
Social Media Marketing Courses in Chennai
Power BI Training in Chennai
Tableau Training in Chennai
This blog is more effective and it is very much useful for me.we need more information please keep update more.
ReplyDeleteHadoop Training in Chennai
Big data training in chennai
Big Data Hadoop Training in Chennai
JAVA Training in Chennai
Python Training in Chennai
Digital Marketing Course in Chennai
Hadoop Training in Tambaram
Big Data Training in Tambaram
Hadoop Training in OMR
Big Data Training in OMR
ReplyDeleteSuperb..! Very comprehensive content for this topic with good explanation. I glad to read your great post, keep doing...
JMeter Training in Chennai
Job Openings in Chennai
Excel Training in Chennai
Embedded System Course Chennai
Spark Training in Chennai
Oracle Training in Chennai
Oracle DBA Training in Chennai
JMeter Training in Porur
Excellent post, it will be definitely helpful for many people. Keep posting more like this.
ReplyDeleteBest ccna Training in Chennai
ccna Training in Chennai
ccna course in Chennai
Angular 7 Training in Chennai
Angular Training in Chennai
Ethical Hacking Training in Chennai
CCNA course in Ambattur
CCNA course in T Nagar
CCNA course in OMR
This comment has been removed by the author.
ReplyDeleteA big thanks for this sharing this awesome post with us. Read it recently and felt very happy on reading every bit of the blog.
ReplyDeleteEnglish Speaking Classes in Mulund
IELTS Classes in Mulund
German Classes in Mulund
French Classes in Mulund
Spoken English Classes in Chennai
IELTS Coaching in Chennai
English Speaking Classes in Mumbai
IELTS Classes in Mumbai
you have provided a amazing post to learn new concepts.
ReplyDeleteethical hacking certification course
Veruy nice
ReplyDeleteinterview-questions/aptitude/permutation-and-combination/how-many-groups-of-6-persons-can-be-formed
tutorials/oracle/oracle-delete
technology/chrome-flags-complete-guide-enhance-browsing-experience/
interview-questions/aptitude/time-and-work/a-alone-can-do-1-4-of-the-work-in-2-days
interview-questions/programming/recursion-and-iteration/integer-a-40-b-35-c-20-d-10-comment-about-the-output-of-the-following-two-statements
ONLINE iNTERNSHIPS
ReplyDeleteWINTER INTERNSHIPS FOR ENGINEERING
SUMMER INTERNSHIP
SUMMER INTERNSHIP IN CHENNAI
WINTER INTERNSHIP IN CHENNAI
INTERNSHIP IN CHENNAI
INTERNSHIP
INTERNSHIPS
IT INTERNSHIP IN CHENNAI
Thank you for sharing. Ethical Hacking training in Chennai by Indian Cyber Security Solutions is a great opportunity for the people of Chennai. A computer hacker is any skilled computer expert that uses their technical knowledge to overcome a problem. Ethical Hacking Course done by ICSS. Indian Cyber Security Solutions is the Best Ethical Hacking Institute in Chennai.
ReplyDeleteNice Blog..
ReplyDeleteiot internships
inplant training in chennai
internship for automobile engineering students
internship for mca students in chennai
internship for eee students
internship for aeronautical engineering students
inplant training report for civil engineering
internship for ece students in chennai with stipend
summer training for ece students after second year
python internship
Good.
ReplyDeletehow to hack flipkart
tp link wifi password hack
power bi developer resume
android secret codes and hacks pdf
slideshow html code for website
javascript max integer
tell me about yourself
given signs signify something and on that basis
kumaran systems interview pattern
bangalore traffic essay
Wonderful thanks for sharing an amazing idea. keep it...
ReplyDeleteGet Best SAP MM Training in Bangalore from Real Time Industry Experts with 100% Placement Assistance in MNC Companies. Book your Free Demo with Softgen Infotech.
Such a great word which you use in your article and article is amazing knowledge. thank you for sharing it.
ReplyDeleteBest SAP S4 HANA Training in Bangalore- eTechno Soft Solutions is a leading SAP S4 HANA Training Institute in Bangalore offering extensive SAP S4 HANA Training by Real-time Working Professionals along with 100% placement support, Booka Free Demo!
ReplyDeleteI have read your blog its very attractive and impressive. I like it your blog.web designing training in bangalore
good...
ReplyDeletedominican republic web hosting
iran hosting
palestinian territory web hosting
panama web hosting
syria hosting
services hosting
afghanistan shared web hosting
andorra web hosting
belarus web hosting
nice...
ReplyDeletebrunei darussalam web hosting
costa rica web hosting
costa rica web hosting
hong kong web hosting
jordan web hosting
turkey web hosting
very informative post..
ReplyDeleteAustralia hosting
Bermuda web hosting
Botswana hosting
mexico web hosting
moldova web hosting
albania web hosting
andorra hosting
armenia web hosting
australia web hosting
nice..post
ReplyDeleteinplant training in chennai
inplant training in chennai
inplant training in chennai for it.php
italy web hosting
very good
ReplyDeleteinplant training in chennai
inplant training in chennai
inplant training in chennai for it.php
Bermuda web hosting
Botswana hosting
armenia web hosting
dominican republic web hosting
iran hosting
palestinian territory web hosting
iceland web hosting
This comment has been removed by the author.
ReplyDeleteThis comment has been removed by the author.
ReplyDeletevery good
ReplyDeleteinplant training in chennai
inplant training in chennai for it
suden web hosting
tunisia hosting
uruguay web hosting
Bermuda web hosting
Botswana hosting
armenia web hosting
lebanon web hosting
This is a topic that's near to my heart... Take care! Exactly where are your contact details though? redmi note 8 pro display replacement bangalore I really love your blog.. Very nice colors & theme. Did you develop this amazing site yourself? Please reply back as I’m planning to create my own personal blog and would love to learn where you got this from or just what the theme is named. Thank you! realme x display replacement
ReplyDeleteI have to thank you for the efforts you've put in writing this website. I really hope to see the same high-grade content from you in the future as well. In truth, your creative writing abilities has encouraged me to get my own website now ;) samsung M30s display replacement I'm very pleased to find this web site. I wanted to thank you for your time due to this fantastic read!! I definitely loved every part of it and I have you saved as a favorite to see new stuff on your website. iphone 11 pro display replacement marathahalli
ReplyDeleteAn intriguing discussion is definitely worth comment. I believe that you should write more on this topic, it may not be a taboo subject but usually people do not talk about such subjects. To the next! All the best!! oneplus 7 pro display replacement bangalore Hello! I simply would like to give you a huge thumbs up for your great information you have got here on this post. I'll be returning to your blog for more soon. vivo V17 pro display replacement marathahalli
ReplyDeleteexcellent blogs.....!!!
ReplyDeletechile web hosting
colombia web hosting
croatia web hosting
cyprus web hosting
bahrain web hosting
india web hosting
iran web hosting
kazakhstan web hosting
korea web hosting
moldova web hosting
I have to voice my passion for your kindness giving support to those people that should have guidance on this important matter.
ReplyDeleteaws training in bangalore
mulesoft training in bangalore
salesforce developer training in bangalore
salesforce admin training in bangalore
servicenow training in bangalore
cloud computing training in bangalore
dell boomi training in bangalore
Excellent post...very useful...
ReplyDeletepython training in chennai
internships in hyderabad for cse 2nd year students
online inplant training
internships for aeronautical engineering students
kaashiv infotech internship review
report of summer internship in c++
cse internships in hyderabad
python internship
internship for civil engineering students in chennai
robotics course in chennai
This comment has been removed by the author.
ReplyDeletehii gud nyc..
ReplyDeleteinternships for cse students in bangalore
internship for cse students
industrial training for diploma eee students
internship in chennai for it students
kaashiv infotech in chennai
internship in trichy for ece
inplant training for ece
inplant training in coimbatore for ece
industrial training certificate format for electrical engineering students
internship certificate for mechanical engineering students
Such an exceptionally valuable article. Extremely intriguing to peruse this article. I might want to thank you for the endeavors you had made for
ReplyDeletecomposing this amazing article.
digital marketing blog
digital marketing course fees
seo training in chennai
digital marketing blogs
blog for digital marketing
blog about digital marketing
digital marketing bloggers
digital marketing resources
search engine optimization guide
free search engine optimization tutorials
free SEO tutorials
seo training tutorials
digital marketing tutorials
free digital marketing resources
free SEO
This was helpful to me thanks for sharing this useful information...
ReplyDeleteDevops Course in Bangalore
Thanks for this blog are more informative contents step by step. I here attached my site would you see this blog.
ReplyDelete7 tips to start a career in digital marketing
“Digital marketing is the marketing of product or service using digital technologies, mainly on the Internet, but also including mobile phones, display advertising, and any other digital medium”. This is the definition that you would get when you search for the term “Digital marketing” in google. Let’s give out a simpler explanation by saying, “the form of marketing, using the internet and technologies like phones, computer etc”.
we have offered to the advanced syllabus course digital marketing for available join now.
more details click the link now.
https://www.webdschool.com/digital-marketing-course-in-chennai.html
Amazing blog useful information.
ReplyDeleteWeb designing trends in 2020
When we look into the trends, everything which is ruling today’s world was once a start up and slowly begun getting into. But Now they have literally transformed our lives on a tremendous note. To name a few, Facebook, WhatsApp, Twitter can be a promising proof for such a transformation and have a true impact on the digital world.
we have offered to the advanced syllabus course web design and development for available join now.
more details click the link now.
https://www.webdschool.com/web-development-course-in-chennai.html
nice job.
ReplyDeleteAnimeflv
nyc blog..
ReplyDeletecoronavirus update
inplant training in chennai
inplant training
inplant training in chennai for cse
inplant training in chennai for ece
inplant training in chennai for eee
inplant training in chennai for mechanical
internship in chennai
online internships
Informative blog post. Thanks for this wonderful Post.
ReplyDeleteSAP Training in Chennai
AWS Training in Chennai
Hardware and Networking Training in Chennai
QTP Training in Chennai
CCNA Training in Chennai
Outstanding blog thanks for sharing such wonderful blog with us
ReplyDeleteDigital Marketing Training Course in Chennai | Digital Marketing Training Course in Anna Nagar | Digital Marketing Training Course in OMR | Digital Marketing Training Course in Porur | Digital Marketing Training Course in Tambaram | Digital Marketing Training Course in Velachery
Great Blog. Thnaks.
ReplyDeleteSAP Training in Chennai
Java Training in Chennai
Software Testing Training in Chennai
.Net Training in Chennai
Hardware and Networking Training in Chennai
AWS Training in Chennai
Azure Training in Chennai
Selenium Training in Chennai
QTP Training in Chennai
Android Training in Chennai
Amazing Article…..
ReplyDeleteReally appreciate your Work
'CCC Service
AC Service in Chennai
Fridge Service in Chennai
Washing Machine Service in Chennai
LED LCD TV Service in Chennai
Microwave Oven Service in Chennai'
เลือกเล่นเกม sa king789 ดีมากกว่าเช่นไร
ReplyDeleteในตอนนี้การเล่นเกมคาสิโนออนไลน์ ดูเหมือนจะคือเรื่องปกติที่ใครๆต่างก็เข้าไปเสาะหาโชคลาภ หาเงินร่วมกันทั้งหมด ซึ่งเกมคาสิโนออนไลน์ในปัจจุบันนี้ก็ได้มีเกมที่น่าดึงดูดเช่น สล็อตออนไลน์ เกมยิงปลา เกมไพ่ หรือเกม sa บาคาร่า ซึ่งเป็นเกมคาสิโนที่กำลังเดินทางมาแรง และก็ทำเงินให้ผู้เล่นก้าวหน้ามากมายทีเดียว ถ้าเกิดคนใดกันพอใจก็สามารถเข้ามาสมัครเลือกเล่นเกมบาคาร่า sa กับเว็บไซต์คาสิโนออนไลน์ของพวกเราได้ตลอด 24 ชั่วโมง แล้วก็วันนี้พวกเราจะมาเสนอแนะเว็บไซต์คาสิโนที่เหมาะสมสำกรับเล่นเกมบาคาร่าออนไลน์ sa ให้ท่านได้ทราบจะ เพื่อที่คุณจะสามารถสร้างความสบาย เพิ่มความสนุกสนานกับการเล่นเกมคาสิโน sa บาคาร่า ได้มากขึ้นกว่าเดิม
เลือกเล่นเกมคาสิโนกับ sa king789
เมื่อคุณอยากเข้ามาเล่นเกมคาสิโนออนไลน์ sa บาคาร่า สามารถเข้ามาเรื่องเล่นเกม sa king789 ซึ่งวันนี้พวกเราจะมาบอกถึงความต่างสำหรับการเล่นเกมบาคาร่ากับ sa king789
• sa king789 เป็นเว็บไซต์เล่นเกมบาคาร่าออนไลน์เชื่อใจได้ ด้วยเหตุว่าเป็นเว็บไซต์ที่เปิดให้บริการมานานมาสมาชิกกว่าหมื่นคนที่ใครๆก็รู้จักนั้นเชื่อมั่นได้เลยว่าเล่นเกม sa บาคาร่ากับพวกเราได้เงินแน่ๆ
• คุณจะได้รับโปรโมชั่นออนไลน์ที่น่าดึงดูดมากมายก่ายกองเมื่อเข้ามาเล่นเกมบาคาร่าที่นี้ เพื่อเป็นการเอาอกเอาใจเหล่าสมาชิกเว็บไซต์ พวกเรามีโปรโมชั่นแจกเครดิตฟรีที่จะให้ท่านได้ประหยัดเงินสำหรับที่คุณจะเอาไปลงทุนเล่นเกมบาคาร่า ทำให้ท่านทำเงินได้มากขึ้นกว่าเดิม
• ระบบเกมของ sa king789 เชื่อถือได้ทุกเกมอ เพราะเหตุว่าเป็นเกมที่ผลิตขึ้นมาจากรชนักนักเขียนโปรแกรมชั้นแนวหน้า
• เว้นแต่บาคาร่าแล้ว sa king789 ยังมีเกมคาสิโนอื่นๆที่น่าดึงดูดมากมายให้ท่านได้ทดลองเล่น ไม่ว่าจะเป็นเกมไพ่ บาคาร่า สล็อต รูเล็ต ก็มีให้ท่านได้เลือกเล่นตามอยาก
• sa king789 มีบริการฝาก ถอน อัตโนมัติ ทำให้ผู้เล่นเกมได้รับความสบาย สบายเยอะขึ้นเรื่อยๆไม่ว่าจะฝาก หรืออยากได้เบิกเงินที่ได้จากการเล่นเกมบาคาร่า
น่าเชื่อเลยว่าถ้าเกิดคุณอยาก หรือพอใจที่จะเข้ามาเล่นเกมบาคาร่ากับ sa king789 คุณจะได้เจอกับความสนุกสนาน ความระทึกใจ และก็สิทธิพิเศษดีๆอีกเพียบเลยที่สามารถช่วยให้ท่านบันเทิงใจ และก็สร้างรายได้จากเว็บไซต์คาสิโนออนไลน์ของพวกเรา แต่คุณสามารถเข้ามาถามไถ่ข้อมูลเพิ่มเติมเกี่ยวกับการเล่นเกมบาคาร่าออนไลน์ถึงที่เหมาะเว็บไซต์คาสิโนออนไลน์ของพวกเรา พวกเรามีคณะทำงานที่จะรอให้การช่วยเหลือในทุกกรรมวิธีสมัครเล่นเกมให้กับคุณ รวมทั้งยังมีแนวทางการเล่นเกม sa ให้ลุกรได้เข้าไปเรียนเพื่อเพิ่มช่องทางทำเงินให้กับคุณได้ ถ้าเกิดคุณไม่ได้อยากพลาดความพิเศษนี้รีบมาสมัครสมาชิกกับ sa king789 ได้เลย
บาคาร่า
Thanks for this blog are more informative contents step by step. I here attached my site would you see this blog.Oneyes Technologies
ReplyDeleteInplant Training in Chennai
Inplant Training in Chennai for CSE IT MCA
Inplant Training in Chennai ECE EEE EIE
Inplant Training in Chennai for Mechanical
Great post! I am actually getting ready to across this information, It’s very helpful for this blog.Also great with all of the valuable information you have Keep up the good work you are doing well.
ReplyDeleteDigital Marketing Online Course
AWS Online Course
Python Online Course
Selenium Online Course
Data Science Online Course
DevOps Online Course
Thank you for sharing this very useful
ReplyDeleteData science Training in bangalore
Aws Training In Bangalore
Hadoop Training In Bangalore
This Was An Amazing ! I Haven't Seen This Type of Blog Ever ! Thank you For Sharing,
ReplyDeleteCivil Service Aspirants
TNPSC Tutorial in English
TNPSC Tutorial in Tamil
TNPSC Notes in English
TNPSC Materials in English
tnpsc group 1 study materials
http://alltopc.com/2020/09/04/12914-webscraper-4-for-mac-free/
ReplyDeleteTESTIMONY ON HOW I GOT MY LOAN FROM A GENUINE FINANCE COMPANY LAST WEEK. Email for immediate response: drbenjaminfinance@gmail.com
ReplyDeleteI am Mrs,Leores J Miguel by name, I live in United State Of America, who have been a scam victim to so many fake lenders online between November last year till July this year but i thank my creator so much that he has finally smiled on me by directing me to this new lender who put a smile on my face this year 2020 and he did not scam me and also by not deceiving or lying to me and my friends but however this lending firm is BENJAMIN LOAN INVESTMENTS FINANCE (drbenjaminfinance@gmail.com) gave me 2% loan which amount is $900,000.00 united states dollars after my agreement to their company terms and conditions and one significant thing i love about this loan company is that they are fast and unique. {Dr.Benjamin Scarlet Owen} can also help you with a legit loan offer. He Has also helped some other colleagues of mine. If you need a genuine loan without cost/stress he his the right loan lender to wipe away your financial problems and crisis today. BENJAMIN LOAN INVESTMENTS FINANCE holds all of the information about how to obtain money quickly and painlessly via Call/Text: +1(415)630-7138 Email: drbenjaminfinance@gmail.com
When it comes to financial crisis and loan then BENJAMIN LOAN INVESTMENTS FINANCE is the place to go please just tell him I Mrs. Leores Miguel direct you Good Luck....
Really awesome blog. Your blog is really useful for me. Thanks for sharing this informative blog. Keep update your blog.
ReplyDeleteDevOps Training in Chennai
DevOps Course in Chennai
Thank you for sharing the blog!! Primavera p6 online course | Online Primavera Course
ReplyDeletethank you.really useful
ReplyDeletedevops Training in chennai | devops Course in Chennai
For online microsoft Certification Exams
ReplyDelete<1--- 1st azure set --->
c
online microsoft azure administrator certification exams edchart
online microsoft azure infrastructure & deployment certification exams edchart
online microsoft azure data analyst certification exams edchart
online microsoft-designing-an-azure-data-solution-certification exams edchart
online microsoft-azure-relational-database-admin-certification exams edchart
online microsoft-azure-iot-developer- certification exams edchart
online designing-and-implementing-microsoft-azure-devops-certification exams edchart
online microsoft-azure-security-technologies-certification exams edchart
edchart
ReplyDeleteFor online microsoft Certification Exams
<1--- 1st azure set --->
online microsoft azure administrator certification exams edchart
online microsoft azure infrastructure & deployment certification exams edchart
online microsoft azure data analyst certification exams edchart
online microsoft-designing-an-azure-data-solution-certification exams edchart
online microsoft-azure-relational-database-admin-certification exams edchart
online microsoft-azure-iot-developer- certification exams edchart
online designing-and-implementing-microsoft-azure-devops-certification exams edchart
online microsoft-azure-security-technologies-certification exams edchart
Java Classes in Ahmedabad
ReplyDeleteJava Classes in Ahmedabad
https://www.liftndrift.com/
ReplyDeleteFinish the Big Data Certification in Chennai from Infycle Technologies, the best software training institute in Chennai which is providing professional software courses such as Data Science, Artificial Intelligence, Java, Hadoop, Selenium, Android, and iOS Development, etc with 100% hands-on practical training. Dial 7502633633 to get more info and a free demo and to grab the certification for having a peak rise in your career.Get Big Data Certification in Chennai | Infycle Technologies
ReplyDeleteEverything is very open with a clear description of the issues. It was definitely informative. Your website is useful. Many thanks for sharing. Feel free to visit my website; 안전놀이터
ReplyDeleteGreat post. keep sharing such a worthy information.
ReplyDeleteSwift Developer Course in Chennai
Swift Training in Bangalore
Learn Swift Online
thanks for providing very important blog.
ReplyDeletewww.nearlearn.com
Cool stuff you have and you keep overhaul every one of us data scientist course in kanpur
ReplyDeleteVery Informative blog thank you for sharing. Keep sharing.
ReplyDeleteBest software training institute in Chennai. Make your career development the best by learning software courses.
power bi training in chennai
Docker Training in Chennai
blue prism training in chennai
android course in chennai
ReplyDeleteThis post is so interactive and informative.keep update more information...
Machine Learning Course in Bangalore
Machine Learning Training in Bangalore
Excellent AWS Training in Chennai, from Infycle Technologies, the best software training institute, and Placement centre in Chennai. And also Providing technical courses likeCyber Security, Graphic Design and Animation, Block Security, Java, Cyber Security, Oracle, Python, Big data, Azure, Python, Manual and Automation Testing, DevOps, Medical Coding etc., with the excellence of training and technical trainers for freshers, experienced, and Tech professionals. with 100+ Live Practical Sessions and Real-Time scenarios. And the students will be sent for placement in the core MNC's. For more details call 7504633633 or 7502633633.
ReplyDeleteThe Best Apps and Games For Android · Apk Module.Extreme Car Driving Simulator Apk
ReplyDeleteThis post is so helpfull and informative.keep updating with more information...
ReplyDeleteFeatures Of Android
Android Platforms
Great Post!!! Thanks for sharing this post with us.
ReplyDeleteLearn AWS Basics
Advantages of AWS
This post is so useful and informative. Keep updating with more information.....
ReplyDeleteIELTS Certification
IELTS Coaching In Bangalore
Great Post!!! thanks for sharing this blog with us.
ReplyDeletewhat is tableau
what is tableau And How Does It Works
This is really impressive post, Embedded Systems Training in Chennai at login360 first acquaint the students with the parts of the Embedded Software and its advancement cycle.
ReplyDeleteThis was helpful to me thanks for sharing this useful information...
ReplyDeleteWeb Designing Course in Chennai
Tableau Training in Chennai
Great post
ReplyDeleterpa training in chennai
Very useful Information.
ReplyDeletetamil novels pdf download
rajesh kumar novels
Thirukkural pdf
tamil story books pdf free download
tamil motivational books pdf download
Learned a lot of new things from your post! Good creation and HATS OFF to the creativity of your mindMSBI Training in Chennai
ReplyDeleteNAME|SSN|DOB|DL|ADDRESS|EMAIL|PHONENUMBER|WORKHISTORY|ACCOUNTDETAILS
ReplyDeleteFresh Fullz & Fresh Spammed
CCNUMBER|MM|YYYY|CVV|NAME|SSN|DOB|ADDRESS|EMAIL|PHONENUMBER
CC fullz with CVV
High Credit Scores Pros 700+
EIN Business Fullz
ICQ 752822040
WA/TG +92 317 272 1122
TG @leadsupplier
Skype/Wickr @peeterhacks
Spamming All fresh Tools & Tutorials
Hacking Stuff
Carding Methods & Cashout Methods
Loan Methods
SMTP's/RDP's/SHELLS/Brutes/C-panels
Key-Loggers/Kali-Linux Full Package
Courses for D**K/D**P Web
SQLi Injector
Combos/I.P's/Proxies
Logs/HQ Emails
ICQ/TG @killhacks
WA +92 317 272 1122
exploit.tools4u at gmail dot com
This comment has been removed by the author.
ReplyDeleteThis is indeed very helpful post for simulation mechanics. Thanks for sharing.
ReplyDeleteWhat a great way to bottle up a huge celebration and make it so memorable. I will be looking forward to adding some of your ideas to my Virtual birthday cards to make them much more desirable in the current times.
ReplyDeleteA leading Indian pharmaceutical company, Apple Therapeutics Private Limited offers a variety of niche, innovative, and research-based high-quality products in a variety of therapeutic categories, including dermatology, cosmetology, trichology, gynecology, paediatrics, diabetes, and nutrition.
ReplyDeleteVisit- https://www.appletherapeutics.in